
Schoenflies Point Groups
Schoneflies published his discription of crystal morphology in 1891 following developments in the subject spanning most of the 19th century. He described 32 point groups that could act as classes (Q classes) for 219 spatial point groups. Each point group expands through translational operations to form a number of spatial point groups that he simply numbered from one to the maximum number for that class. This notation was replaced in crystallographic use by the Hermann-Maguin (International) system because in that system it is possible to describe individual space groups. A surprising consequence of these events is that later development work in molecular symmetry continued to use the Schoenflies system after crystallographers had discarded it. It evolved in a time before the composition of matter composed of atoms was understood. It remains the dominant approach to the subject of molecular symmetry even though it is a very cumbersome, time-wasting system. Images of molecules arranged in the Laue class layout allow the various operations to be pictured.
Molecular symmetry is described by the three dimensional point groups in the table on the right. Each point group in the table belongs to a spatial partition described as asymmetric, symmetric or spherical and within this division to a point group system based on the main axial order of the group. Asymmetric and symmetric rotational groups consist of cyclic and dihedral groups of increasiing order. Cyclic groups have just one generator, a rotation about the main axis,and repeated applications of this generator produce the operations of the group. Dihedral groups include a second generator, a 2-fold rotation at right angles to the main axis, and combinations of this generator produce the 2n operations of these groups. Each system is divided into one or two Laue classes that appear in the table as rows of point groups. So, the tetragonal system divides into cyclic and dihedral Laue classes. Spherical molecules have multiple rotational axes that are not necessarily at right angles to each other although some are. The tetrahedral and octahedral Laue classes are related in a similar way to that of the cyclic and dihedral groups in the less symmetric partitions. All octahedral groups have an index-2 tetrahedral subgroup that provides an underlying symmetry and the relationship between the two is similar to that of the dihedral and cyclic groups.
Top classes themselves are divided into rows of Laue classes based on subsidiary axial orders that may be present. Each Laue class contains a set of groups defined by a rotational group G containing generator rotations. The next column contains semi-direct product groups that contain the same rotational operations as the defining group but in which one of the rotational generators is combined with spatial inversion. Groups in the two middle columns belong to exactly the same abstract group structure as the rotational group G because spatial inversion does not alter the way in which rotational elements combine. Obviously, each of these groups has the same number of elements - the group order. Obviously Schoenflies derived his notation by observing the external shapes of crystals because his work preceeded the discovery of atomic structure. His system is based on solid forms such as prisms and anti-prisms described by rotations combined with vertical and horizontal mirror planes. The lower table on the right shows how Schoenflies rationalized crystal structures into many series of symbols that seem to be rtather arbitrary.
Groups of the final column (Gi) contain twice the number of elements, consisting of the rotational elements of that Laue class together with each of those elements combined with spatial inversion. These groups contain the space inversion operation itself and are of twice the order of other groups in the class. The order of any group is therefore quickly found from the table on the right but it is difficult to deduce this information from the Schoeflies symbols themselves.
Max Von Laue was awarded the Nobel prize for the discovery of x-ray crystallography in 1914 and in further work he showed that x-ray images added a centre of symmetry to whatever symmetry the crystal itself might have. Laue classes then became the primary method of showing point groups identical abstract structure with their centred supergroup.
Irreducible representations
A major problem with the Schoenflies system is that groups are labeled in a way that has little connection with their group structure. Look, for example, at the hexagonal dihedral groups in the table and notice the curious mixture of 6's, 3's, C's and D's even though these groups have the same abstract structure and therefore the same irreducible representations. Using the Schoenflies system, symmetry operations in a three dimensional space are described by their equivalent spatial transformations and the resulting matrices are reduced to irreps with the aid of "the great orthogonality theorem" a procedure that occupies many pages of text books. The resulting irreps are labeled with the aid of a notation first produced by Robert Mulliken in 1933 in which distinct irreps are defined for each separate point group because Schoneflies does not connect similar abstract groups. Its all a bit of a mess.
Schoneflies/Muliken irrep notation follows Schoneflies point group notation, which is unrelated to the abstract group structure and so introduces lots of different irrep symbols. However, symmetry groups in a Laue class follow the same multiplication table and therefore have the same irreps because it is the abstract group that defines irreps It follows that irreps of a given Laue class can all use the same irrep symbols. In fact all the Laue classes can share a single simple system.
Asymmetric group representations can always be reduced to a number of 1-dimensional irreps. Symmedtric group representations reduce to 1 and 2 dimensional irreps while sherical groups reduce to 1,2 and 3 dimenisional irreps.

Schoneflies uses five operations to define point groups
- Identity - doing nothing or rotating the molecule by 360 degrees about any axis.
- Rotation about an axis - forms cyclic and dihedral groups
- Mirror plane of symmetry - in the vertical or horizontal axes.
- Center of symmetry - abbreviated i.
- Rotation-reflection axis - a combination of rotation about an an axis and a reflection.
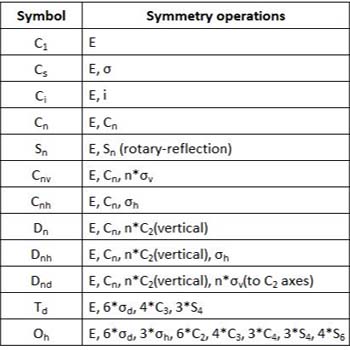
table courtesy of symmetrynaik
Notice that Schoenflies uses mirror reflection to describe point groups then develops this operation into a rotation-reflection operation. An alternative system might instead use the inversion operation and see reflection as a consequence of combining rotational operations with inversion. The latter approach has enormous advantages: the inversion operation commutes with all rotational operations while the reflection operation does not. In fact inversion is the only non-rotational operation required any point group in a three demensional space.
Some mappings of Schoneflies/Mulliken notation to the simple Laue group notation are possible
